Distribution of quadratic forms

The distribution of a quadratic form in p standard Normal variables is a linear combination of p chi-squared distributions with 1df. When there is uncertainty about the variance, a reasonable model for the distribution is a linear combination of F distributions with the same denominator.

pchisqsum(x, df, a, lower.tail = TRUE, 
   method = c("satterthwaite", "integration","saddlepoint"))
pFsum(x, df, a, ddf=Inf,lower.tail = TRUE, 
   method = c("saddlepoint","integration","satterthwaite"), ...)

Arguments

x

Observed values

df

Vector of degrees of freedom

a

Vector of coefficients

ddf

Denominator degrees of freedom

lower.tail

lower or upper tail?

method

See Details below

...

arguments to pchisqsum

Value

Vector of cumulative probabilities

Details

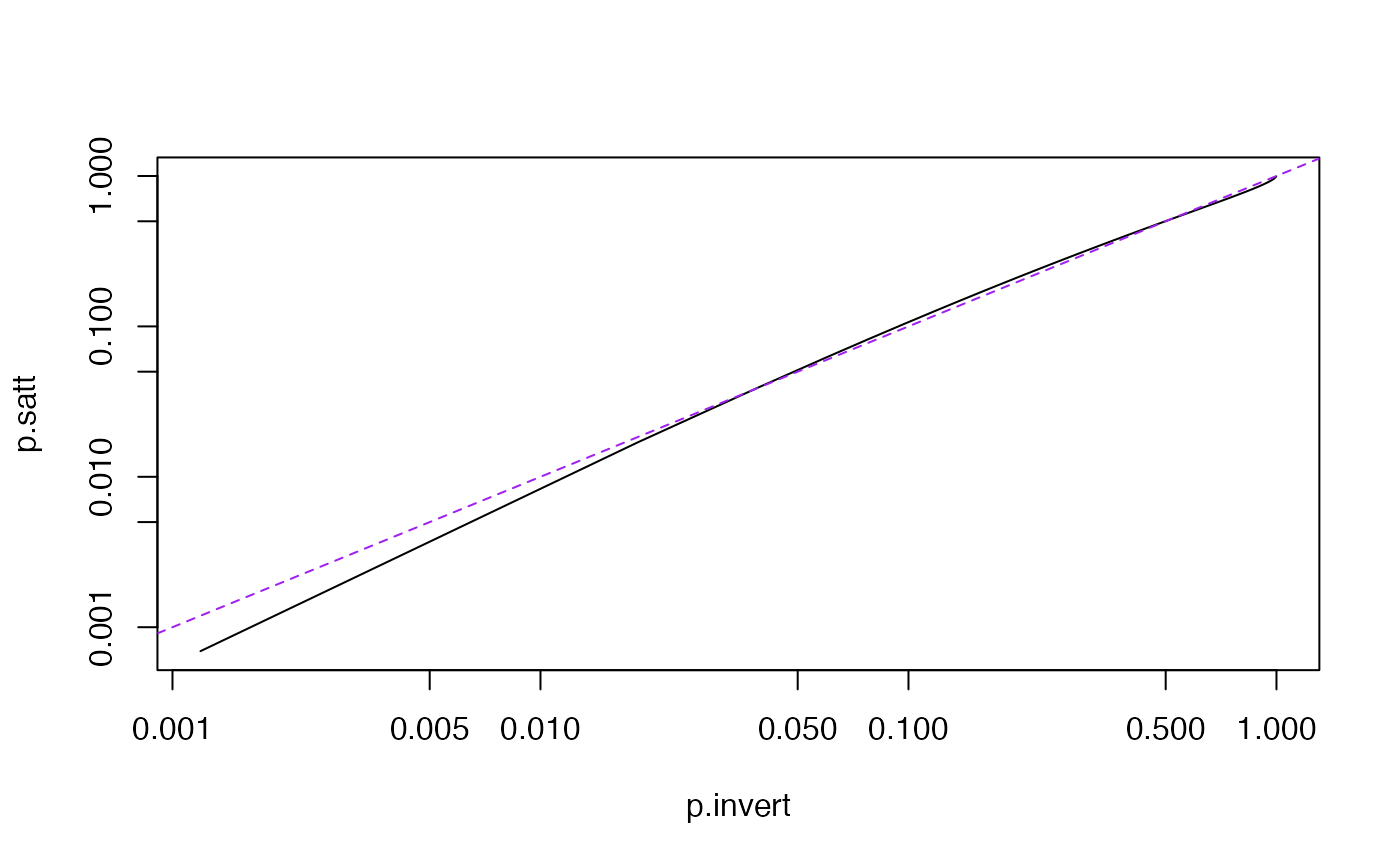
The "satterthwaite" method uses Satterthwaite's approximation, and this is also used as a fallback for the other methods. The accuracy is usually good, but is more variable depending on a than the other methods and is anticonservative in the right tail (eg for upper tail probabilities less than 10^-5). The Satterthwaite approximation requires all a>0.

"integration" requires the CompQuadForm package. For pchisqsum it uses Farebrother's algorithm if all a>0. For pFsum or when some a<0 it inverts the characteristic function using the algorithm of Davies (1980). These algorithms are highly accurate for the lower tail probability, but they obtain the upper tail probability by subtraction from 1 and so fail completely when the upper tail probability is comparable to machine epsilon or smaller.

If the CompQuadForm package is not present, a warning is given and the saddlepoint approximation is used.

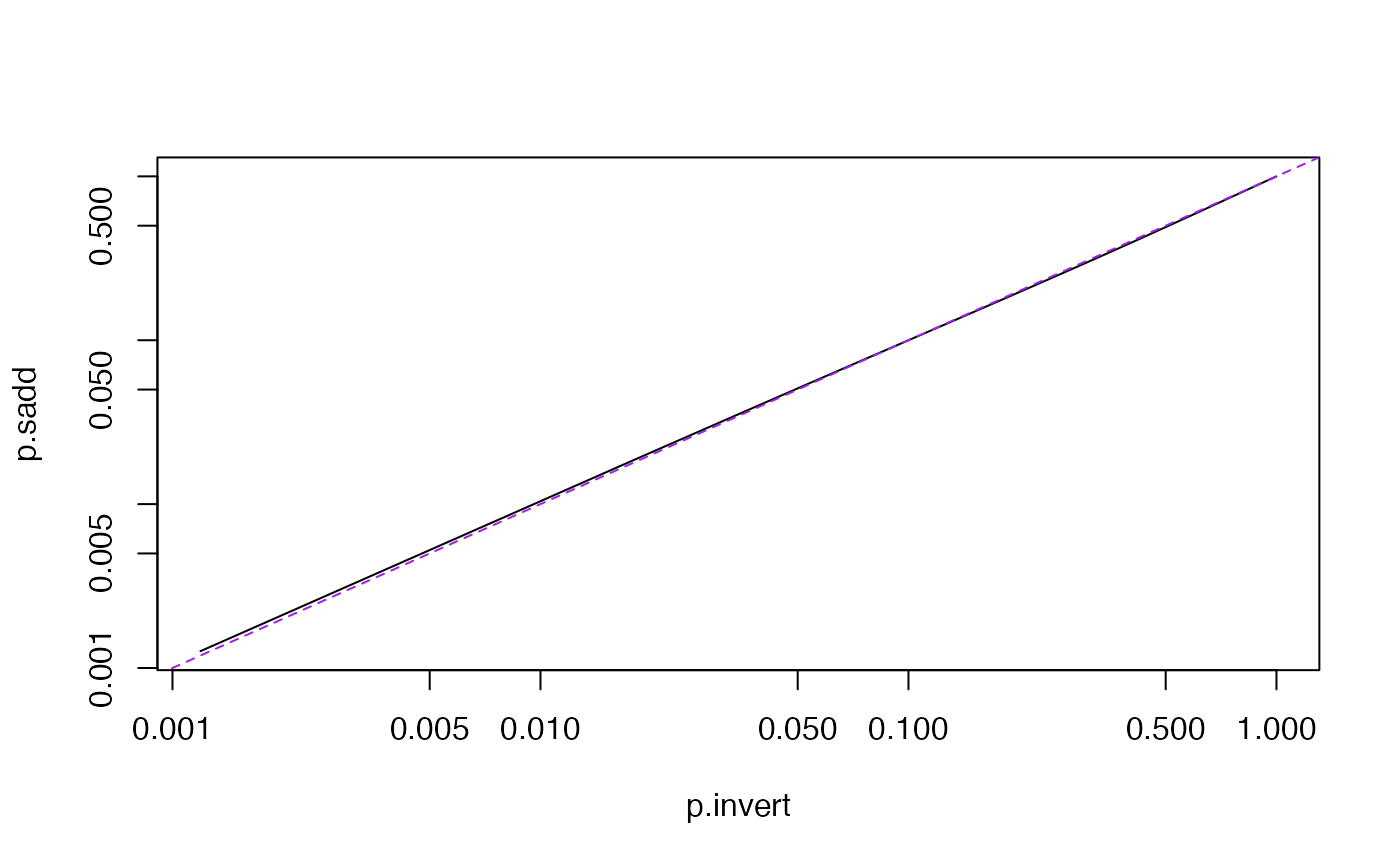
"saddlepoint" uses Kuonen's saddlepoint approximation. This is moderately accurate even very far out in the upper tail or with some a=0 and does not require any additional packages. The relative error in the right tail is uniformly bounded for all x and decreases as p increases. This method is implemented in pure R and so is slower than the "integration" method.

The distribution in pFsum is standardised so that a likelihood ratio test can use the same x value as in pchisqsum. That is, the linear combination of chi-squareds is multiplied by ddf and then divided by an independent chi-squared with ddf degrees of freedom.

References

Chen, T., & Lumley T. (2019). Numerical evaluation of methods approximating the distribution of a large quadratic form in normal variables. Computational Statistics and Data Analysis, 139, 75-81.

Davies RB (1973). "Numerical inversion of a characteristic function" Biometrika 60:415-7

Davies RB (1980) "Algorithm AS 155: The Distribution of a Linear Combination of chi-squared Random Variables" Applied Statistics,Vol. 29, No. 3 (1980), pp. 323-333

P. Duchesne, P. Lafaye de Micheaux (2010) "Computing the distribution of quadratic forms: Further comparisons between the Liu-Tang-Zhang approximation and exact methods", Computational Statistics and Data Analysis, Volume 54, (2010), 858-862

Farebrother R.W. (1984) "Algorithm AS 204: The distribution of a Positive Linear Combination of chi-squared random variables". Applied Statistics Vol. 33, No. 3 (1984), p. 332-339

Kuonen D (1999) Saddlepoint Approximations for Distributions of Quadratic Forms in Normal Variables. Biometrika, Vol. 86, No. 4 (Dec., 1999), pp. 929-935

See also

pchisq

Examples

x <- 2.7*rnorm(1001)^2+rnorm(1001)^2+0.3*rnorm(1001)^2
x.thin<-sort(x)[1+(0:50)*20]
p.invert<-pchisqsum(x.thin,df=c(1,1,1),a=c(2.7,1,.3),method="int" ,lower=FALSE)
p.satt<-pchisqsum(x.thin,df=c(1,1,1),a=c(2.7,1,.3),method="satt",lower=FALSE)
p.sadd<-pchisqsum(x.thin,df=c(1,1,1),a=c(2.7,1,.3),method="sad",lower=FALSE)

plot(p.invert, p.satt,type="l",log="xy")
abline(0,1,lty=2,col="purple")

plot(p.invert, p.sadd,type="l",log="xy")
abline(0,1,lty=2,col="purple")


pchisqsum(20, df=c(1,1,1),a=c(2.7,1,.3), lower.tail=FALSE,method="sad")
#> [1] 0.009519523
pFsum(20, df=c(1,1,1),a=c(2.7,1,.3), ddf=49,lower.tail=FALSE,method="sad")
#> [1] 0.01322202
pFsum(20, df=c(1,1,1),a=c(2.7,1,.3), ddf=1000,lower.tail=FALSE,method="sad")
#> [1] 0.009688087